1. Введение
2. Основные структуры
- 2.1 Элементы теории множеств
- 2.2 Операции с множествами
- 2.3 Функции и способы их задания
- 2.4 Числовые последовательности
3. Пределы. Непрерывные функции
- 3.1 Предел последовательности
- 3.1.1 Определения
- 3.1.2 Арифметика пределов
- 3.1.3 Арифметика бесконечно малых
- 3.1.4 Признаки существования пределов
- 3.1.5 Вычисление пределов
- 3.1.6 Замечательный предел
- 3.2 Функции непрерывной переменной
- 3.2.1 Определения
- 3.2.2 Арифметика пределов
- 3.2.3 Арифметика бесконечно малых
- 3.2.4 Признаки существования пределов
- 3.2.5 Замечательные пределы
- 3.2.6 Список важнейших предельных соотношений
- 3.3 Непрерывные функции
- 3.3.1 Определения
- 3.3.2 Основные свойства
- 3.3.3 Разрывы функции
4. Производная, дифференциальное исчисление
- 4.1 Производная
- 4.1.1 Определение производной
- 4.1.2 Производная от элементарных функций
- 4.1.3 Производная от суммы, произведения и частного функций
- 4.1.4 Производные от сложной функции, от обратной функции, от функции, заданной параметрически
- 4.1.5 Таблица производных
- 4.2 Первый дифференциал
- 4.2.1 Определение и основные свойства первого дифференциала
- 4.2.2 Геометрический смысл первого дифференциала
- 4.2.3 Дифференциал сложной функции. Инвариантность первого дифференциала
- 4.3 Свойства дифференцируемых функций
- 4.4 Правило Лопиталя и раскрытие неопреленностей
5. Высшие производные
- 5.1 Определение и свойства высших производных
- 5.2 Определение и свойства дифференциалов высших порядков
- 5.3 Теорема Тейлора
- 5.4 Формула Тейлора для некоторых функций
6. Приложения дифференциального исчисления
- 6.1 Монотонность функции и знак ее производной
- 6.2 Достаточное условие локального максимума/минимума
- 6.3 Решение задачи о глобальном максимуме/минимуме функции на замкнутом отрезке
- 6.4 Выпуклость вверх, выпуклость вниз, точки перегиба
7. Первообразная (неопределенный интеграл)
- 7.1 Определение и основные свойства первообразных
- 7.2 Таблица основных первообразных
- 7.3 Интегрирование по частям
- 7.4 Замена переменной в первообразной
8. Техника вычисления первообразных
- 8.1 Интегралы от дробно-рациональных функций
- 8.1.1 Полиномы, основные свойства
- 8.1.2 Дробно-рациональные функции, основные свойства
- 8.1.3 Выделение целой части и разложение на простейшие для дробно-рациональных функций
- 8.1.4 Вычисление первообразной от дробно-рациональной функции
- 8.2 Интегралы от тригонометрических функций
- 8.3 Интегралы от функций, содержащих иррациональности
- 8.4 Подстановки Эйлера
- 8.5 "Неберущиеся" интегралы
9. Определенный интеграл
- 9.1 Определение
- 9.2 Геометрический смысл определенного интеграла
- 9.3 Основные свойства
- 9.4 Формула Ньютона-Лейбница
- 9.4.1 Интеграл как функция верхнего предела
- 9.4.2 Формула Барроу
- 9.4.3 Формула Ньютона-Лейбница
- 9.5 Интегрирование по частям в определенном интеграле
- 9.6 Замена переменной в определенном интеграле
10. Несобственные интегралы
- 10.1 Несобственные интегралы 1 рода
- 10.1.1 Определение и основные свойства
- 10.1.2 Признаки сходимости несобственных интегралов 1 рода
- 10.2 Несобственные интегралы 2 рода
- 10.2.1 Определение и основные свойства
- 10.2.2 Признаки сходимости несобственных интегралов 2 рода
11. Интегралы зависящие от параметра
12. Приложения определенных интегралов
4. Производная, дифференциальное исчисление
4.3 Свойства дифференцируемых функций
Теорема. Если функция $f(x)$ дифференцируема в точке $x_0$, то эта функция непрерывна в точке $x_0$.
Доказательство.
Замечание. Обратное утверждение не верно: непрерывная функция не обязана быть дифференцируемой. Т.о., дифференцируемость "более сильное" свойство, чем непрерывность.
Определение. Пусть функция $y=f(x)$ задана на интервале $(a,b)$, $x_0 \in (a,b)$. Говорят, что функция $y=f(x)$ имеет в точке $x_0$ локальный максимум, если для некоторой окрестности этой точки $U$ справедливо: $f(x) \leq f(x_0)$ при всех $x \in U$. Аналогичным образом определяется локальный минимум.
Теорема Ферма. Пусть функция $y=f(x)$ задана на интервале $(a,b)$, $x_0 \in (a,b)$, причем $f(x)$ дифференцируема в точке $x_0$. Если $f(x)$ имеет в точке $x_0$ локальный максимум (или локальный минимум), то $f'(x_0)=0$.
Доказательство.
Теорема Ферма является необходимым условием наличия в точке $x_0$ локального максимума или локального минимума функции $f(x)$ - этим условием является равенство $f'(x_0)=0$. Для вывода достаточного условия нам потребуется несколько более продвинутая техника, оно обсуждается ниже. В связи с этими условиями возникает следующее определение.
Определение.Стационарной точкой (или: экстремальной точкой) функции $f(x)$ называется такая точка $x_0$, которая удовлетворяет условию $f'(x_0)=0$.
Теорема Ролля. Пусть функция $f(x)$ удовлетворяет следующим условиям.
1. Она непрерывна на интервале $\left [ a,b\right ]$.
2. Она дифференцируема на интервале $(a,b)$.
3. $f(a)=f(b)$.
Тогда на интервале $\left [ a,b\right ]$ найдется точка $c$ такая, что $f'(c)=0$.
Доказательство.
Рассмотрим геометрическую интерпретацию теоремы Ролля.
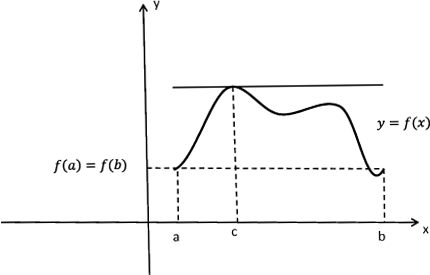
Рис 4: К геометрическому смыслу теоремы Ролля
На рисунке 4 изображена функция, принимающая равные значения на концах. В соответствии с заключением теоремы, существует точка $c$, в которой касательная к графику функции параллельна оси $x$ (т.е. $f'(c)=0$).
Теорема Лагранжа. Пусть функция $f(x)$ удовлетворяет следующим условиям.
1. Она непрерывна на интервале $\left [ a,b\right ]$.
2. Она дифференцируема на интервале $(a,b)$.
Тогда на интервале $\left [ a,b\right ]$ найдется точка $c$ такая, что \begin{equation} f'(c)=\frac{f(b)-f(a)}{b-a}. (11) \label{Lagr} \end{equation}
Доказательство.
Формула (11) называется формулой конечных приращений. Ее можно переписать в виде: \[ f(b)-f(a)=f'(c)\cdot (b-a), \] где, напомним, $c \in (a,b)$.
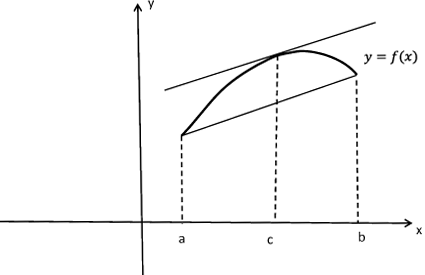
Рис 5:К геометрическому смыслу теоремы Лагранжа
В таком виде она часто используется в том случае, когда требуется вычислить (или оценить) величину $f(b)-f(a)$.
Рассмотрим геометрическую интерпретацию теоремы Лагранжа, см. рис. 5. Значение $f'(c)$ фиксирует угол наклона касательной к графику в точке $c$, выражение $(f(b)-f(a))/(b-a) $ задает угол наклона хорды, соединяющей концы кривой. Таким образом, теорема Лагранжа утверждает, что между $a$ и $b$ найдется такая точка $c$, что каcательная к графику в этой точке параллельна хорде, соединяющей концы кривой.
Теорема Коши. Пусть функции $f(x),g(x)$ удовлетворяют следующим условиям.
1. Они непрерывны на интервале $\left [ a,b\right ]$.
2. Они дифференцируемы на интервале $(a,b)$, причем $g(a) \neq g(b)$.
Тогда на интервале $\left [ a,b\right ]$ найдется точка $c$ такая, что
\[
\frac{f'(c)}{g'(c)}=\frac{f(b)-f(a)}{g(b)-g(a)}.
\]
Доказательство.
Теорема Лагранжа является частным случаем теоремы Коши в том случае, когда $g(x)=x$.