1. Введение

+2. Основные структуры

2.1 Элементы теории множеств
2.2 Операции с множествами
2.3 Функции и способы их задания
2.4 Числовые последовательности

3. Пределы. Непрерывные функции +

3.1 Предел последовательности
3.1.1 Определения
3.1.2 Арифметика пределов
3.1.3 Арифметика бесконечно малых
3.1.4 Признаки существования пределов
3.1.5 Вычисление пределов
3.1.6 Замечательный предел
3.2 Функции непрерывной переменной
3.2.1 Определения
3.2.2 Арифметика пределов
3.2.3 Арифметика бесконечно малых
3.2.4 Признаки существования пределов
3.2.5 Замечательные пределы
3.2.6 Список важнейших предельных соотношений
3.3 Непрерывные функции
3.3.1 Определения
3.3.2 Основные свойства
3.3.3 Разрывы функции

4. Производная, дифференциальное исчисление+

4.1 Производная
4.1.1 Определение производной
4.1.2 Производная от элементарных функций
4.1.3 Производная от суммы, произведения и частного функций
4.1.4 Производные от сложной функции, от обратной функции, от функции, заданной параметрически
4.1.5 Таблица производных
4.2 Первый дифференциал
4.2.1 Определение и основные свойства первого дифференциала
4.2.2 Геометрический смысл первого дифференциала
4.2.3 Дифференциал сложной функции. Инвариантность первого дифференциала
4.3 Свойства дифференцируемых функций
4.4 Правило Лопиталя и раскрытие неопреленностей

5. Высшие производные+

5.1 Определение и свойства высших производных
5.2 Определение и свойства дифференциалов высших порядков
5.3 Теорема Тейлора
5.4 Формула Тейлора для некоторых функций

6. Приложения дифференциального исчисления+

6.1 Монотонность функции и знак ее производной
6.2 Достаточное условие локального максимума/минимума
6.3 Решение задачи о глобальном максимуме/минимуме функции на замкнутом отрезке
6.4 Выпуклость вверх, выпуклость вниз, точки перегиба

7. Первообразная (неопределенный интеграл)+

7.1 Определение и основные свойства первообразных
7.2 Таблица основных первообразных
7.3 Интегрирование по частям
7.4 Замена переменной в первообразной

8. Техника вычисления первообразных+

8.1 Интегралы от дробно-рациональных функций
8.1.1 Полиномы, основные свойства
8.1.2 Дробно-рациональные функции, основные свойства
8.1.3 Выделение целой части и разложение на простейшие для дробно-рациональных функций
8.1.4 Вычисление первообразной от дробно-рациональной функции
8.2 Интегралы от тригонометрических функций
8.3 Интегралы от функций, содержащих иррациональности
8.4 Подстановки Эйлера
8.5 "Неберущиеся" интегралы

9. Определенный интеграл+

9.1 Определение
9.2 Геометрический смысл определенного интеграла
9.3 Основные свойства
9.4 Формула Ньютона-Лейбница
9.4.1 Интеграл как функция верхнего предела
9.4.2 Формула Барроу
9.4.3 Формула Ньютона-Лейбница
9.5 Интегрирование по частям в определенном интеграле
9.6 Замена переменной в определенном интеграле

10. Несобственные интегралы+

10.1 Несобственные интегралы 1 рода
10.1.1 Определение и основные свойства
10.1.2 Признаки сходимости несобственных интегралов 1 рода
10.2 Несобственные интегралы 2 рода
10.2.1 Определение и основные свойства
10.2.2 Признаки сходимости несобственных интегралов 2 рода

11. Интегралы зависящие от параметра+

12. Приложения определенных интегралов+

12.1 Площадь плоских фигур
12.2 Длина дуги кривой
12.3 Вычисление объема тел
12.4 Приложения в механике
Глава 11

12. Приложения определенных интегралов

12.3 Вычисление объема тел

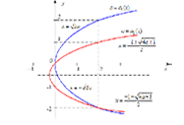
С помощью определенного интеграла можно вычислять объем тела. Рассмотрим тело, расположенное вдоль оси $x$, от точки $a$ до точки $b$. Предположим, что известна $S(x)$ - площадь сечения тела плоскостью, перпендикулярной оси $x$. Нарежем наше тело на "блинчики" плоскостями, перпендикулярными оси $x$, на рис. 11 изображен один такой "блинчик" толщины $\Delta x$.

Рис 11: Объем тела.

Объем такого "блинчика" приближенно равен $S(x)\Delta x$. Складывая объемы таких "блинчиков", получаем приближенно объем тела - интегральную сумму вида

\[ \Sigma = \sum _{k=1}^NS(x_k)\Delta x_k\,. \]

Переходя к пределу при $max _k \Delta x_k \rightarrow 0$, получаем интеграл, который и принимается (по определению) за объем тела:

\[ V=\int _a^bS(x)dx\,. \]

Если тело получено вращением кривой $y=f(x)$ вокруг оси $x$, площадь поперечного сечения нетрудно вычислить: $S(x)=2\pi f^2(x)$, так что для объема тела вращения получаем

\[ V=2\pi \int _a^bf^2(x)dx\,. \]

Пример.

Вычислим объем эллипсоида - тела, границу которой составляет поверхность с уравнением

\[ \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1. \]

Рассмотрим сечение этого тела плоскостью, перпендикулярной оси $x$. Для этого достаточно фиксировать $x, x\in \left[-a,\, a \right ]$ и рассмотреть уравнение границы соответствующей фигуры,

\[ \frac{y^2}{b^2}+\frac{z^2}{c^2}=1-\frac{x^2}{a^2}. \]

Это уравнение несложно переписать в виде

\[ \frac{y^2}{b^2(1-\frac{x^2}{a^2})}+\frac{z^2}{c^2(1-\frac{x^2}{a^2})}=1, \]

и опознать в этой фигуре эллипс на плоскости $(y,z)$ с полуосями $b \sqrt{1-\frac{x^2}{a^2}}, \quad c \sqrt{1-\frac{x^2}{a^2}}$. Площадь эллипса мы вычисляли выше, так что, в соответствии с полученными выше результатами, площадь поперечного сечения эллипсоида равна

\[ S(x)=\pi bc\cdot \left (1-\frac{x^2}{a^2} \right ). \]

Таким образом, объем эллипсоида равен

\[ V=\int _{-a}^aS(x)\, dx=\pi bc\cdot\int _{-a}^a\left (1-\frac{x^2}{a^2} \right )\, dx=\pi bc \cdot \left (x-\frac{x^3}{3a^2} \right )|_{-a}^a= \] \[ \frac{4}{3}\pi a b c. \]

Задачи.

1. Вычислить объем тела, образованного вращением вокруг оси $x$ фигуры, ограниченной параболами $y=x^2$ и $y^2=x$. $y=ln(1-x^2)$ от $x=0$ до $x=1/2$.

2. Вычислить объем тела, образованного вращением вокруг оси $y$ фигуры, ограниченной параболами $y=x^2$ и $y=2-x^2$.

3. Вычислить объем тела, образованного вращением вокруг оси $x$ фигуры, ограниченной кривыми $y=(1+x^2)^{-1}$, $y=x/2$ и $x=0$.

4. Вычислить объем тела, образованного вращением вокруг оси $x$ кривой $y=\sin x$, $0 \leq x \leq \pi$.

5. Вычислить объем тела, образованного вращением вокруг оси $y$ фигуры, ограниченной параболами $y=2x-x^2$ и $y=0$.