3. Пределы. Непрерывные функции

3.1.1 Определения

Определение. Конечное число $A$ называется пределом последовательности $a_n$, если для любого $\varepsilon >0$ существует $N(\varepsilon)\in \mathbb{N}$ такое, что при $n>N(\varepsilon)$ выполняется: $|a_n-A|<\varepsilon $.

Обозначение. Этот факт обозначают \[ \lim _{n\rightarrow +\infty}a_n=A, \]

или

\[ a_n \xrightarrow[n\to +\infty]{} A. \]

Пример

Не все последовательности имеют предел. Например, можно проверить, что последовательность $a_n=(-1)^n$ не имеет предела.

Контрольный вопрос

Определение. Говорят, что последовательность $a_n$ имеет пределом $+\infty$, если для любого $A>0$ существует такое $N$, что при всех $n>N$ выполняется неравенство $a_n>A$.

Обозначение. Этот факт обозначают \[ \lim _{n\rightarrow +\infty}a_n=+\infty, \]

или

\[ a_n \xrightarrow[n\to +\infty]{} +\infty. \]

Аналогично определяется ситуация, когда $ \lim _{n\rightarrow +\infty}a_n=-\infty$.

Определение. Если предел последовательности равен $0$, последовательность называют бесконечно малой. Если предел последовательности равен $\infty$, последовательность называют бесконечно большой.

Теорема. Пусть последовательность $a_n$ имеет конечный предел. Тогда $a_n$ - ограниченная последовательность.

Доказательство.

Теорема. Пусть последовательность $a_n$ имеет конечный предел $A$, \[ a_n \xrightarrow[n\to +\infty]{} A. \]

Тогда последовательность $b_n=(a_n-A)$ является бесконечно малой.

Теорема. Последовательность может иметь только один предел.

Доказательство.

3.1.2 Арифметика пределов

Здесь приведена серия теорем, описывающая предел суммы, произведения и частного последовательностей, имеющих конечный предел.

Теорема. Пусть \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}b_n=B, \]

причем $A$ и $B$ - конечные числа. Тогда последовательность $(a_n+b_n)$ имеет конечный предел, причем

\[ \lim _{n\rightarrow +\infty}(a_n+b_n)=A+B. \]

Доказательство.

Теорема. Пусть \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}b_n=B, \]

причем $A$ и $B$ - конечные числа. Тогда последовательность $(a_n\cdot b_n)$ имеет конечный предел, причем

\[ \lim _{n\rightarrow +\infty}(a_n\cdot b_n)=A\cdot B. \]

Теорема. Пусть \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}b_n=B, \]

причем $A$ и $B$ - конечные числа, $B \neq 0$. Тогда последовательность $(a_n / b_n)$ имеет конечный предел, причем

\[ \lim _{n\rightarrow +\infty}(a_n / b_n)=A / B. \]

Теорема. Пусть при всех $n$ выполняется $a_n < M$ для какого-то числа $M<\infty$, причем последовательность $a_n$ имеет конечный предел, \[ \lim _{n\rightarrow +\infty}a_n=A. \]

Тогда $A \leq M$ (переход в неравенствах к пределу).

Замечание. Разумеется, существуют аналоги этих теорем и в том случае, когда один из пределов (или оба предела) бесконечен.

Контрольный вопрос.

3.1.3 Арифметика бесконечно малых

Теорема. Пусть $a_n$, $b_n$ - бесконечно малые при $n \rightarrow +\infty$. Тогда $(a_n+b_n)$ - бесконечно малая при $n \rightarrow +\infty$.

Теорема. Пусть $a_n$ - бесконечно малая при $n \rightarrow +\infty$, $b_n$ - ограниченная последовательность. Тогда $a_n\cdot b_n$ - бесконечно малая при $n \rightarrow +\infty$.

Теорема. Пусть $a_n$ - бесконечно малая при $n \rightarrow +\infty$, \[ \lim _{n\rightarrow +\infty}b_n=B, \] причем $B$ - конечное число, $B \neq 0$. Тогда последовательность $(a_n / b_n)$ бесконечно малая при $n \rightarrow +\infty$.

Определение. Бесконечно малые $a_n$, $b_n$ называются эквивалентными, если существует предел \[ \lim _{n\rightarrow +\infty}a_n/b_n=\theta, \] причем $\theta \neq 0$, $\theta \neq \pm \infty$. Этот факт обозначают следующим образом: $a_n \sim b_n$ при $n \rightarrow +\infty$.

3.1.4 Признаки существования пределов

Следующие теоремы указывают условия, при которых последовательность имеет предел.

Теорема. Пусть $a_n$ - монотонно возрастающая последовательность, ограниченная сверху. Тогда она имеет конечный предел.

Следствие. Если $a_n$ - монотонно возрастающая последовательность, она имеет пределом либо $=+\infty$, либо конечное число. Соответственно, для монотонно убывающей последовательности.

Теорема. Пусть $a_n$ - монотонно убывающая последовательность, ограниченная снизу. Тогда она имеет конечный предел.

Теорема. Пусть для всех $n$ выполняются неравенства $a_n\leq b_n \leq c_n$, и \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}c_n=A. \] Тогда $b_n$ также имеет предел, причем \[ \lim _{n\rightarrow +\infty}b_n=A. \]

Критерий Коши. Для того, чтобы последовательность $a_n$ имела конечный предел, необходимо и достаточно, чтобы для любого $ \varepsilon >0$ существовало такое $N$, что при всех $m,n>N$ выполнялось $|a_n-a_m|<\varepsilon $.

3.1.5 Вычисление пределов

Здесь мы приведем несколько примеров вычисления пределов последовательностей. При этом мы используем приведенные выше теоремы об арифметике пределов.

1. \[ a_n=(n+1)^2/n^2. \] Напомним, что $1/n \xrightarrow[n\to +\infty]{} 0$, так что $1/n^2=1/n\cdot 1/n \xrightarrow[n\to +\infty]{} 0$. Итого \[ a_n=\frac{n^2+2n+1}{n^2}=1+2\cdot \frac{1}{n}+\frac{1}{n^2}\xrightarrow[n\to +\infty]{} 1. \]

2. \[ a_n=\frac{2n^3-100n^2+1}{100n^2-23n}. \] Выделяем в числителе и знаменателе старшие степени переменной $n$, стремящейся к $+\infty$: \[ a_n=\frac{n^3(2-100\frac{1}{n}+\frac{1}{n^3})}{n^2(100-23\frac{1}{n})}=n\cdot\frac{(2-100\frac{1}{n}+\frac{1}{n^3})}{(100-23\frac{1}{n})}. \] Скобка в числителе имеет пределом при $n \rightarrow +\infty$ число 2, скобка в знаменателе имеет пределом число 100. Множитель $n$ стремится к $+\infty$, так что в итоге имеем: \[ a_n \xrightarrow[n\to +\infty]{} +\infty. \]

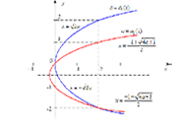
3. \[ a_n=\sqrt{n^2+6n+1}-\sqrt{n^2+2n-4}. \] Умножим числитель и знаменатель этого выражения на "сопряженное" выражение, \[ a_n= \] \[ \frac{(\sqrt{n^2+6n+1}-\sqrt{n^2+2n-4})}{\sqrt{n^2+6n+1}+\sqrt{n^2+2n-4}}. \] \[ \frac{(\sqrt{n^2+6n+1}+\sqrt{n^2+2n-4})}{\sqrt{n^2+6n+1}+\sqrt{n^2+2n-4}}= \] \[ \frac{n^2+6n+1-(n^2+2n-4)}{\sqrt{n^2+6n+1}+\sqrt{n^2+2n-4}}= \] \[ \frac{4n+5}{\sqrt{n^2+6n+1}+\sqrt{n^2+2n-4}} \] Затем выносим старшую степень $n$ в числителе и в знаменателе, \[ a_n= \] \[ \frac{n(4+\frac{5}{n})}{n(\sqrt{1+\frac{6}{n}+\frac{1}{n^2}}+\sqrt{1+\frac{2}{n}-\frac{4}{n^2}})}= \] \[ \frac{4+\frac{5}{n}}{\sqrt{1+\frac{6}{n}+\frac{1}{n^2}}+\sqrt{1+\frac{2}{n}-\frac{4}{n^2}}}. \]

Предел числителя равен 4, предел знаменателя равен 2. В итоге находим: \[ a_n \xrightarrow[n\to +\infty]{} 2. \]

Задачи.

3.1.6 Замечательный предел

Теорема. \begin{equation} \lim _{n\rightarrow +\infty}\left(1+\frac{1}{n}\right )^n=e, (4) \end{equation} где $e$- конечное число, $e=2.71828...$ (это число $e$ служит основанием натуральных логарифмов).

Доказательство.